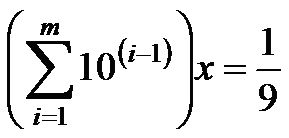
ということになる.よし,掌握.
[個人用ページ] :
一言 「獣の数字?」
初出: 2006/06/06 T.Shirai
更新: 2006/06/06 T.Shirai
ウソではありません.いまは’06年06月06日PM06時06分です(本当に偶然です.分単位は狙いましたが).数字マニアという訳では全くありませんが,やはりキリの良い数字は好きですね(注).さて,今週は中間試験です.私も自分の授業以外の一般科目の試験監督も行ないます.今日は数学I(1年生)でした.今回の試験問題は暇つぶしには非常に良く,かなり悩ませて貰いました(もちろん,きちんと監督もした上です).
(注)
私にとって,64,128,256,512,1024,2048,4096もキリの良い数字なのですが,一般社会で賛同を得るのは困難です.
その中の一問,しばらく解けませんでした.
| (循環数) | 6.060606.... を分数で表せ. |
答えは 200/33 です.どう解けば良いのかと言えば以下の通り.
(1) 6.060606...=66.66666...−60.606060...
唐突ですが,これはOKですよね.
(2) ちなみに,66.66666....=(2/3)×100 ですね.
(3) ここで,x=6.06060... とおくと,60.606060...=10
x
つまり,
(4) x = (2/3)×100 − 10x と,(1)から(3)から言えますので,これを移項したりしてまとめると,
(5) 11x = (2/3)×100 = 200/3
(6) x = 200/33
ということです.
なるほど,循環数か.思い付くのは1/3が0.33333....であるということ.ここからスタートして色々と考えたが答えに辿り付かなかった.ネックは,1/3の”循環の単位が一桁”であること.
(循環の単位が一桁)
ここから考えつくのは”好きな循環数を作るには何か基本ルールがあるはずだ”.
1/3を3で割れば0.1111111...
つまり(1/9)×nとすれば(nは一桁の自然数),0.11111...から0.99999...まで好きな1桁の循環数になる.
(循環の単位が二桁)
次に思い付いたのが0.01010101...は何だろう?
6.0606060606...=200/33を導出したアルゴリズムを用いれば,これは1/99.
(念のために)
x = 0.01010101....
x = 0.11111.... − 10x
11x = 1/9
x = 1/99
つまり(1/99)×nとすれば(nは二桁の自然数),0.010101...から0.999999....までの好きな二桁の循環数になる.
オリジナルの問題をこの考え方で解けば,
6.06060606... = (1/99)×6+6 = (6+6×99)/99 = (2+2×99)/33 = 200/33
合っていますね.ヨカッタ.
(循環の単位が三桁)
もう言うまでも無いですが,(1/999)×n(nは三桁の自然数)で良い.試しに電卓で(1/999)×123とすれば,
0.12312312312312312312312312312312...(CALC.EXE) た,たのしいぞ.
(念のために)
x = 0.001001001....
x = 0.1111... − 100
x − 10 x
111 x = 1/9
x = 1/999
(循環の単位がm桁)
ここまでのところをまとめると,
| 一桁の時: | x = 1/9 | → 100 x = 1/9 |
| 二桁の時: | x +10 x = 1/9 | → (100 +101) x = 1/9 |
| 三桁の時: | x +10 x + 100 x = 1/9 | → (100 +101 +102 ) x = 1/9 |
つまり,帰納法(でいいのかな)で考えると,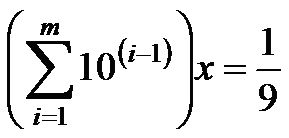
ということになる.よし,掌握.
(蛇足)キミの頭がダメダメならばコンピュータに任せればOK,なのか?
世界最大の素数を分散コンピューティングで探し出すプロジェクトが存在する.
GIMPS http://www.mersenne.org/
http://www2.117.ne.jp/~mat/dcomp/gimps/index.html
私はBOINCに参加しているので,こちらにはノータッチですが,2005年末に「42番目のメルセンヌ素数2^25964951-1(781万6230桁)発見」したらしい.
6.060606...の問題を10分間考えても解けなかったので,同じように巨大な循環数を表す分数をコンピュータで探し出そうか,などと,考えたのですが,まぁ,解き方が分かったので止めました.しかし,もしコンピュータで求めるとしたらどうすれば良いのだろうか.分母,分子を総当りで調べる,つまり1/1からスタートして,9999999..../9999999....という風にそれぞれ1ずつ増やして行くのだろう.
問題は,
(1)「循環数になっているか,どうかをどのように判断するのか」
(2)「どの組み合わせは無駄だから飛ばすのか」
でしょう.たとえば,x/y=12341234123412341234....と(たかだか倍精度程度の浮動小数点型で得られた計算結果が)続いていても,計算精度を超えたその先で...12349...と崩れている可能性がある.計算をコンピュータに任せる訳にはいかない.ヒトが手で計算するように計算させて,余りが”以前と同じ数字”になっていることを判断して,初めて循環していると判断できる.
| (例) 123/999 123/999 = 0 余り 123 1230/999 = 1 余り 231 (=1230−999) 2310/999 = 2 余り 312 (=2310−1998) 3120/999 = 3 余り 123 (=3120−2997) お,一致した.循環だ. |
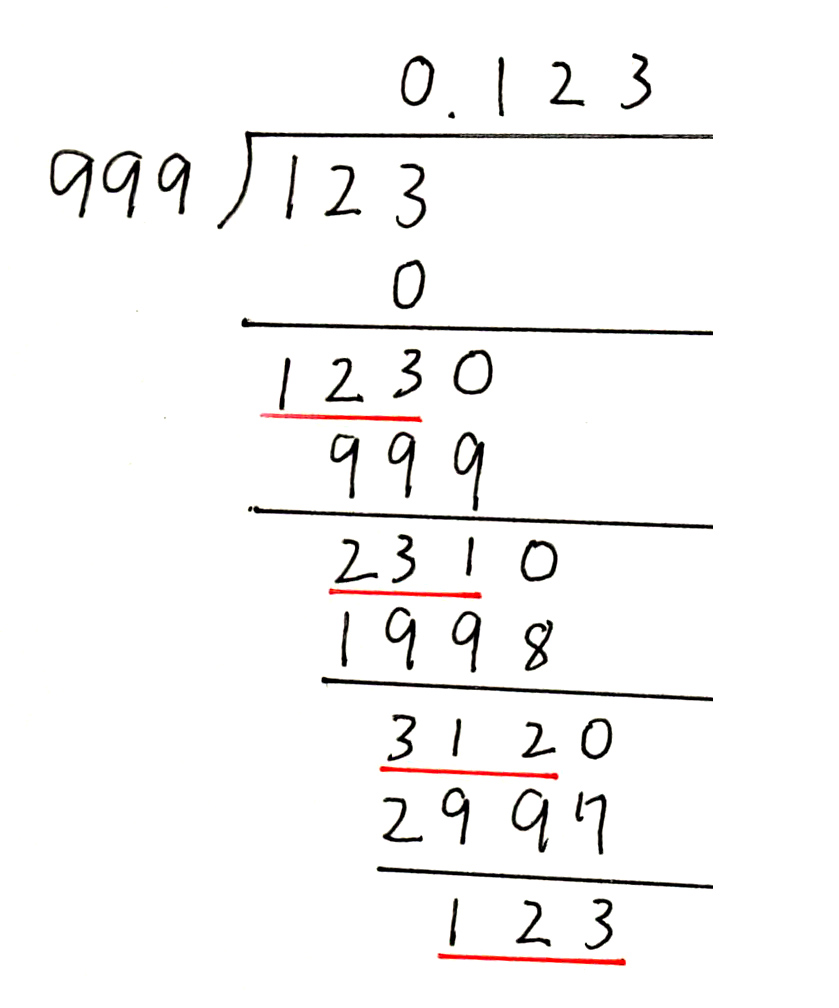 |